やさしい理系物理
§1 一次元の運動学
1 高校物理とは?
世界の謎
時は18世紀末、——まだ原子や分子も見つかっておらず、その存在について科学者の中でも議論が分かれていた頃です。そこでは、古典物理学(高校物理)という学問が大きな成功を収めていました。
古典物理学とは、「力学」「電磁気学」「熱力学」の3つで、この世界のすべての現象は説明できる、という一連の試みのことです。残念ながら、この試みは原子・分子のような微視的スケールでは全く役に立たないことが明らかになり、20世紀以降の量子力学・相対性理論の発展へと繋がっていきます。
しかし、逆に言えば、我々の日常のような(マクロな)スケールに限定すれば、古典物理はきわめて便利で実用的な学問だ、ということです。また、——奇妙なことに——大学に入って量子力学・相対性理論などを学ぶときも、古典物理学は予備知識として必須となります。高校物理では、これら古典物理学を中心に学んでいくことになります。
物理学の目的は、つまるところ、この世界のすべての現象を、(数式により)寸分たがわす正確に記述することです。この世界の物理法則とは、一体何でしょうか。空間や質量とは、一体何なのでしょうか。
たんにテスト・受験のためのつまらない勉強だと捉えず、ノンフィクションの推理小説と思って読んでもらえると幸いです。
2 速度・加速度
座標と空間
本題に入る前に、座標系についての話をしましょう。
力学を始めるときは、まずはこの世界(空間)に座標を張ります。座標を張ることによって「この粒子は位置 $(x,y)$ にいるぞ!」と分かり、初めて数式で運動を記述できるわけです。このように、世界に「固定」した座標のことを、物理では特に座標系といいます。
なぜかは良く分かりませんが、この世界はどうやら、空間は3次元です。つまり、空間には「縦・横・高さ」という $3$ つの直交した方向があって、それぞれに対応する変数 $(x,y,z)$ を指定することで、粒子の位置を指定できます。これはまぎれもない観測事実です。
なぜこの世界が $3$ 次元なのかは、現代物理でもよく分かっていませんが、そこを疑っていても何も進まないので、認めて先に進むことにしましょう。なお、初めから $3$ 次元の物理を考えていても複雑で仕方がないので、今後しばらくは1次元(数直線)上のみの運動を考えることにします。
質点
眼の前の消しゴムを考えてください。それには有限の大きさ・形や弾性など、色々な性質がありますが、これらを一挙に考えていると複雑でたまりません。そこで、今後しばらくは、大きさも形もない、理想的な点粒子を考えることにしましょう。これを物理では、質点と呼びます。
導入
数直線上( $x$ 軸上)の質点の運動を考えましょう。図1を見て下さい。時刻 $t$ における質点の位置は、 $t$ の関数として $x(t)$ と書くことができます。ここで関数とは、入力値 $x$ を $1$ つ決めると出力値 $f(x)$ も $1$ つに決まるようなもののことです。質点の位置 $x(t)$ は、時間 $t$ の関数になっています。
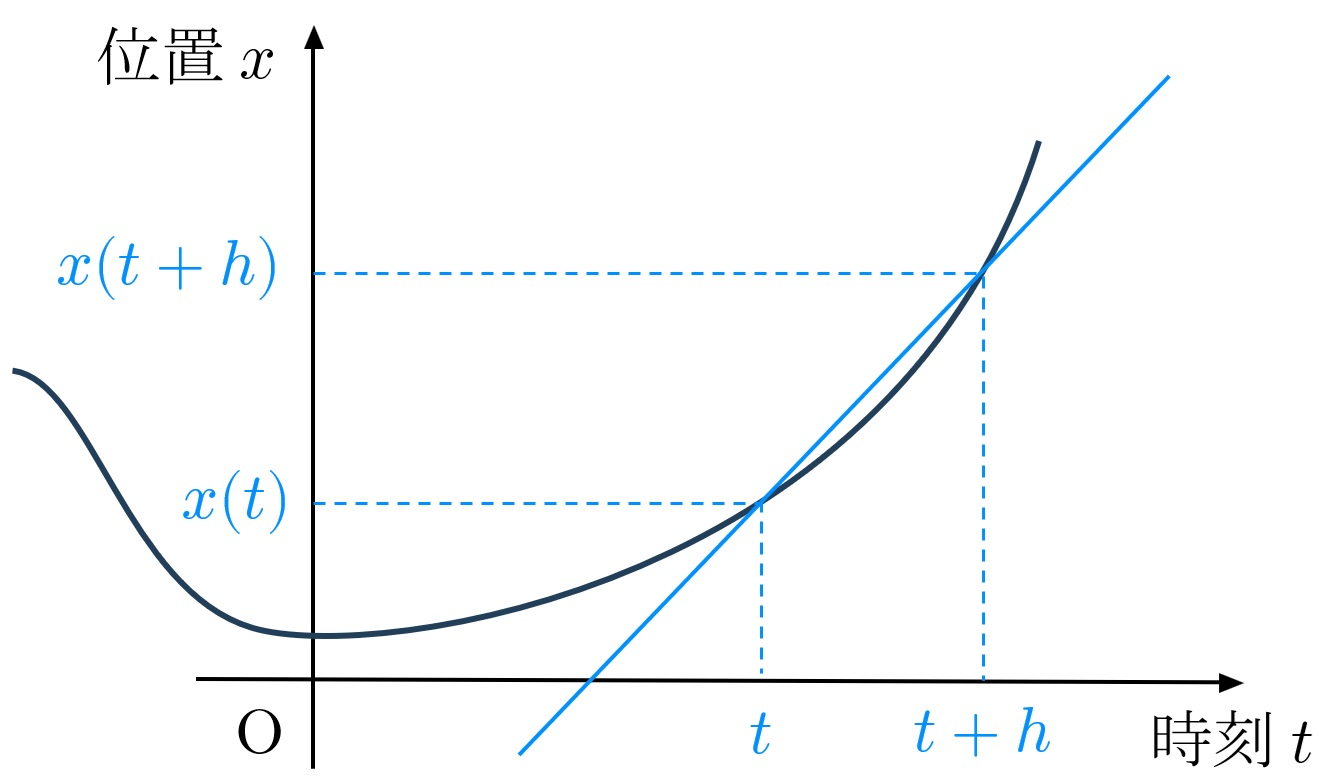
図1 速度の説明。黒い線が関数 $x(t)$ であり、位置を表す。
次に、速度について考えましょう。ある時刻 $t$において位置 $x(t)$ にあった質点が、少し時間が進んで時刻 $t+h$ では位置 $x(t+h)$ にいたとします。このとき、平均の速度を \begin{align} v(t,h)=\frac{x(t+h)-x(t)}{h} \end{align} として定義します。平均の速度 $v(t,h)$ は、図式的には図2における青色の直線の傾きに相当します。
平均の速度において、時間の間隔 $h$ を $0$ に近づけるときの $v(t,h)$ の極限値
\begin{align} v(t)=\lim_{h \to 0}\frac{x(t+h)-x(t)}{h} \end{align}
を、時刻 $t$ における瞬間の速度といいます。
上の式の形が、微分の定義式になっていることに注意してください。言い換えると、速度は、時間に関する微分になっています。これを数式であらわに書くと、以下のようになります。
\begin{align} v(t)=\frac{\mathrm{d} x(t)}{\mathrm{d} t} \end{align}
いわば、速度というのは、時間を横軸にしたときのグラフ $y=x(t)$ の傾きを意味しているわけです。同様にして、速度の時間微分として加速度 $a(t)$ を以下のように定義します。
\begin{align} a(t)=\frac{\mathrm{d} v(t)}{\mathrm{d} t}=\frac{\mathrm{d}^2 x(t)}{\mathrm{d} t^2} \end{align}
加速度というのは、その名前のとおり、どのくらい質点が「加速」しているのかを示すものです。例えば通勤電車は、 毎秒約$3\mathrm{km/h}$ くらいで加速しながら駅を出発します。
定義
位置 $x=x(t)$ の質点の速度 $v=v(t)$、加速度 $a=a(t)$ を下記により定義する。
\begin{align} v=\frac{\mathrm{d} x}{\mathrm{d} t}、\quad a=\frac{\mathrm{d} v}{\mathrm{d} t} \end{align}注意
高校物理では、速度 $v$ の絶対値 $|v|$ を特に速さといいます。
一旦速度・加速度を上のように定義してしまえば、その積分により位置・速度を「逆算」できます。例えば、時刻 $t=t_0$ にて質点の位置 $x(x_0)$、およびその後の速度 $v(t)$ が与えられているとき、$x(t)$ は下記のように記述できます。
\begin{align} x(t)&=x(t_0) + \int_{t_0}^t v(t')\mathrm{d}t' \end{align}
例
加速度が $a(t)=a_0$(定数)で与えられる質点の動きを考えよう。質点の速度 $v(t)$は、
とかける。ただし、$x_0=x(t_0)$である。
3 最後に:微積分の記号について
最後に、物理でよく使う微積分の「感覚」について説明しておきましょう。
注意
本節の内容は、数学的に厳密な議論ではないことに注意してください。ここでの目的は、数学的に厳密な議論をすることではなく、微積分についての感覚、物理的直観を身につけることにあります。
本節の結論を簡単に述べると、以下のようになります。
(1) $\mathrm{d}x$ とは、「めっちゃ小さい $x$ 」である。
(2) 微分とは、割り算である。
(3) 積分とは、足し算である。
これについて、以下で説明します。
微分とは、割り算である
これまでと同様に、質点の動きを考えましょう。位置 $x(t)$ にある質点が、少し進んで時刻 $t+\mathrm{d}t$ では位置 $x(t+\mathrm{d}t)$ にいたとします。先ほどと違うのは、 $\mathrm{d}t$ はものすごく小さい量である、ということです。大学では、このような量を微小量と呼ぶことがあります(言葉は覚える必要ありません)。
時刻 $t$ から $t+\mathrm{d}t$ までの間で、質点の位置は $x(t+\mathrm{d}t)-x(t)$ だけ変化したことになります。ここで、そもそも $\mathrm{d}t$ はものすごく小さい量だったので、この変化量 $x(t+\mathrm{d}t)-x(t)$ もものすごく小さい量(微小量)のはずです。このような意味を込めて、この量を $\mathrm{d}x$ と書くことにします:
積分とは、足し算である
次に、速度 $v(t)$ から位置 $x(t)$ を逆算する方法を考えましょう。先程と同様に、時刻 $t$ から $t+\mathrm{d}t$ までのすごく短い間を考えます。この間に、質点の速度は $v(t)$ 一定値とみなしてよいでしょう。すると、時刻 $t$ から $t+\mathrm{d}t$ の間に質点が進んだ距離 $\mathrm{d}x$ は、速度 $v(t)$ と $\mathrm{d}t$ をかけて \begin{equation} \begin{split} \mathrm{d}x = v(t)\mathrm{d}t \end{split} \end{equation} とかけます。これを時刻 $t_0$ から $t_1$ まで、ひたすら無限に足しまくればよいわけです。
この「無限に足しまくる」というのを、記号で $\displaystyle \int$ と書くことにしましょう。足し算なので本来はシグマ記号 $\displaystyle \sum$ を使うべきですが、今回は「無限に小さい量を無限に足している」ので、異なる記号を用いています。これにより、上の式は \begin{equation} \begin{split} \int_{x(t_0)}^{x(t_1)} \mathrm{d}x = \int_{t_0}^{t_1} v(t)\mathrm{d}t \end{split} \end{equation} となります。左辺を整理して、 \begin{equation} \begin{split} x(t_1) = x(t_0) +\int_{t_0}^{t_1} v(t)\mathrm{d}t \end{split} \end{equation} となるわけです。右辺第二項の計算は積分と呼ばれます。無限に小さい量を無限に足し上げる(積み上げる)イメージですね。
