やさしい理系物理
§2 スカラーとベクトル
ここでは、物理で重要な概念であるスカラー、ベクトルについて、なるべく数式を使わずに理解を深めます。
1 (不正確な)一般の説明
まずは、高校物理の参考書でよくされている「雑な説明」をします。後に述べますが、この説明はかなり不正確ですので、忙しい方は飛ばしても大丈夫です。
スカラー
実数で表される量のことをスカラー量(あるいはたんにスカラー)といいます。例えば、質量や電荷などはスカラー量です。ようは、スカラーというのは、私達が知っている普通の「数」で表される量のことですね。
ベクトル
スカラーに対して、向きと大きさを持った量をベクトル量(あるいはたんにベクトル)といいます。ようは、高校数学で習う「ベクトル」により表される量のことですね。例えば、位置ベクトルや速度などはベクトル量です。
例として、位置ベクトルについて説明しましょう。$3$ 次元空間において質点の位置は、$x,y,z$ 座標の値 $(x,y,z)$ を指定することにより記述できます。これを、$3$ 次元の空間ベクトルとして、以下のように書くことにします。
\begin{align} \overrightarrow r = (x,y,z) \end{align}
これを位置ベクトルといいます。なぜ座標ではなくてベクトルとして記述するかというと、「量」という概念で扱うことができる、という単純な理由です。ベクトルって座標と違って、足し算とかできますよね。
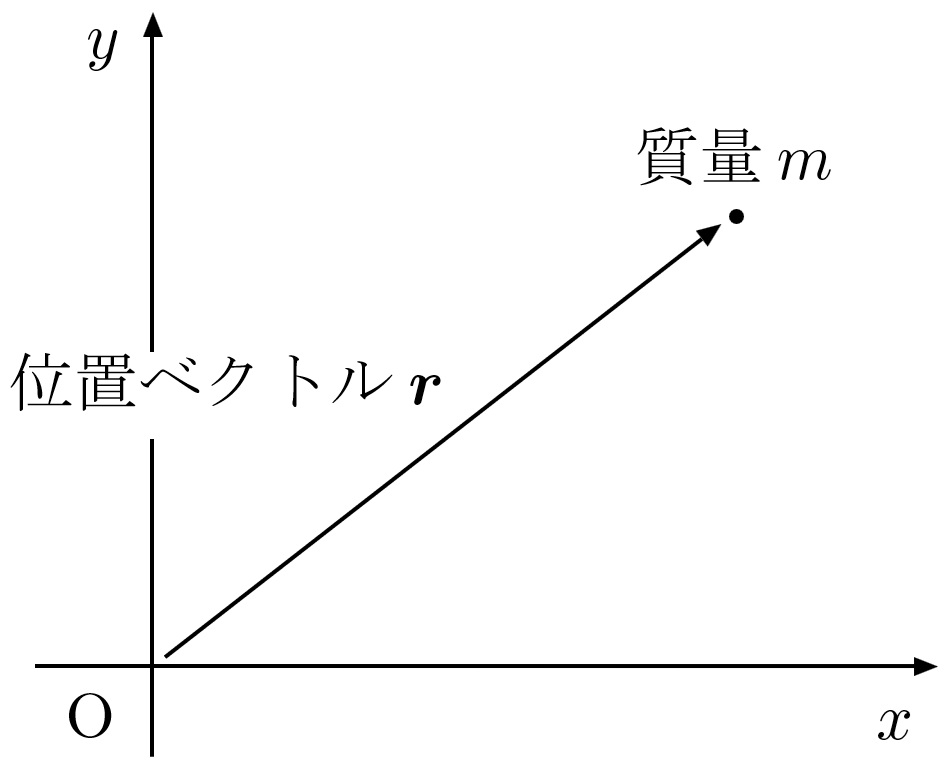
図1 スカラー量である質量と、ベクトル量である位置ベクトルを表した図。
2 より正確な説明
上の説明は、実のところかなり不正確で、物理的に本質的な意味を欠いています。ここでは、物理的な本質を含んだ「スカラー、ベクトル」の概念について、数式を使わない説明をします。以下の考え方は、今後入試問題を解くうえでも、重要な理解になるでしょう。
座標系
本題に入る前に、座標系についての話をしましょう。
力学を始めるときは、運動を記述するために、まずはこの世界に座標を張ります。座標を取ることによって「この粒子は位置 $(x,y,z)$ にいるぞ!」と分かり、初めて数式で運動を記述できるわけです。このように、世界に「固定」した座標のことを、物理では特に座標系といいます。
当然、座標系の取り方というのは色々あります。下図2のように、初めに定めた座標系( $S$ 系)に対して、速度 $v$ で動いているような座標系(上図、$S'$ 系)を取ることもできますし、回転している座標系(下図、$S''$ 系)を取ることもできます。
$S'$ 系は、路上で立つ人に対して、時速 $40\mathrm{km}$ のタクシーに乗っている人が貼った座標系に対応します。一方で、$S''$ 系は、路上で静止している人の周りをクルクル回っている(円運動している)座標系に対応します。
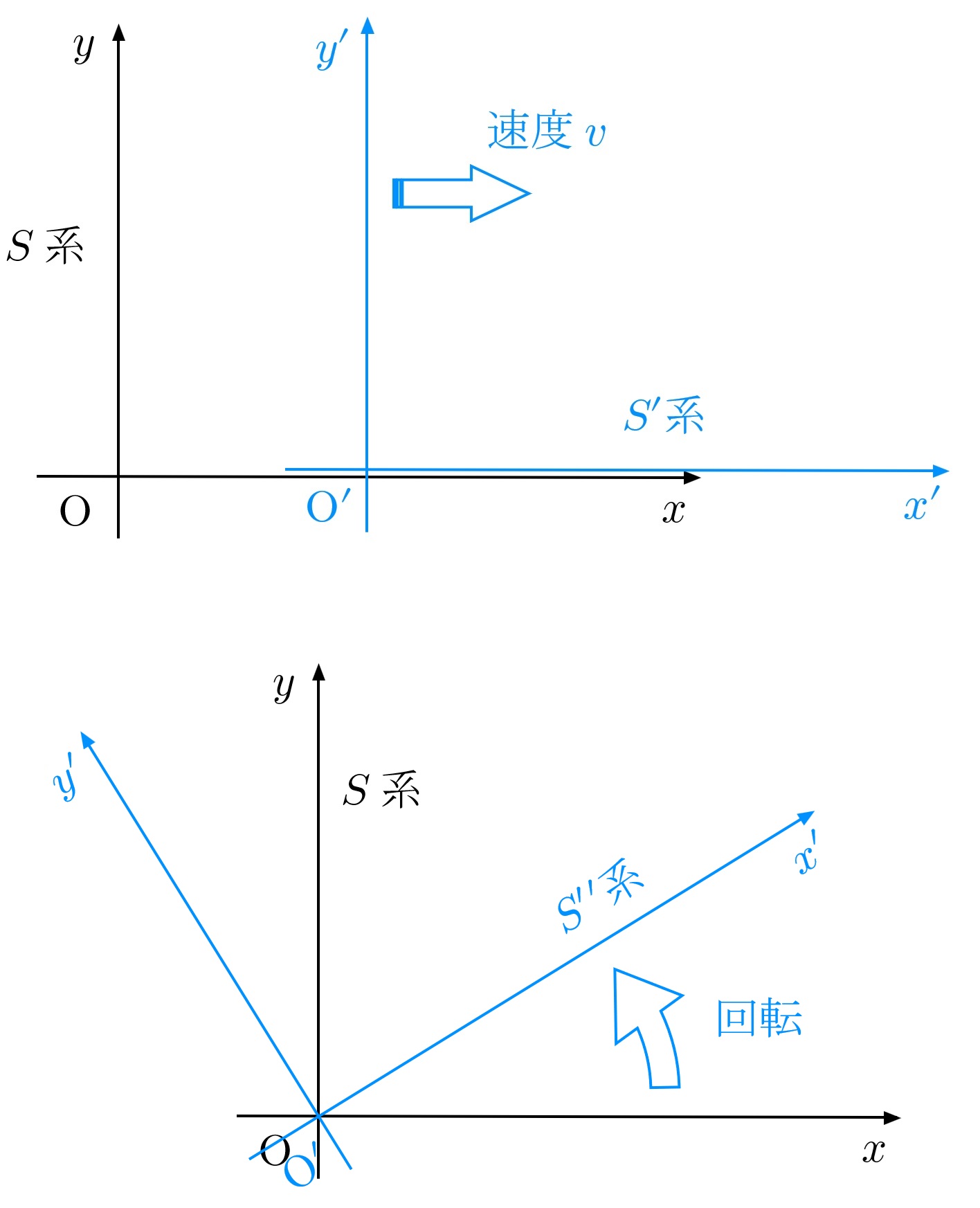
図2 いろいろな座標の取り方。
このように書くと、あたかも「$S$ 系というのは基準になる座標系で、$S'$ 系や $S''$ 系というのはひねくれた座標系の取り方だ」と考えるかもしれませんが、そんな事はありません。考えてみれば、$S'$ 系から見ても $S$ 系というのは速度 $v$ で動いているわけです。
このように、$S$ 系を特別扱いする理由というのはなく、すべての座標系(座標の取り方)は相対的であるというのが、現代の物理学の標準的な見方です。
相対性原理
さて、ここまでで、いろんな座標系の視点に立つ人を見てきました。ここで、いろいろな座標系から、共通の物理現象を見てみましょう。例えば、マグネシウムに火を付けると激しく燃える現象を、$S$ 系、$S'$ 系など、いろんな座標系から記述してみるわけです。
当然ながら、座標のとり方が違うので、$S$ 系、$S'$ 系では、この現象は異なる数式で記述されることが予想されます。しかし、どちらも同じ現象を眺めているのですから、記述される現象は本質的には同じはずです。言い換えると、現象を記述する根本となる物理法則は、座標の取り方によらず不変でなくてはいけません。このような考え方を、相対性原理といいます。
補足
相対性原理というと、アインシュタインの相対性理論のことを連想する人がいるかも知れません。おっしゃるとおりで、アインシュタインの相対性理論は、相対性原理に従う理論の $1$ つです。ただし相対性原理はより一般的に、現代の物理学がもつきわめて一般的な立場の $1$ つであると言えます。
スカラー
座標の話を色々したところで、スカラーの話に戻ります。下図3を見てください。「5」と書かれた札を、$S$ 系、$S'$ 系の両方から眺めることにします。ここでは、$S$ 系を地上から眺めている人、$S'$ 系を飛行機の上から眺めている人、ということにしましょうか。
どちらの人から見ても、書かれているプラカードには「5」と書かれています(当たり前ですね!)。このような量をスカラー量といいます。
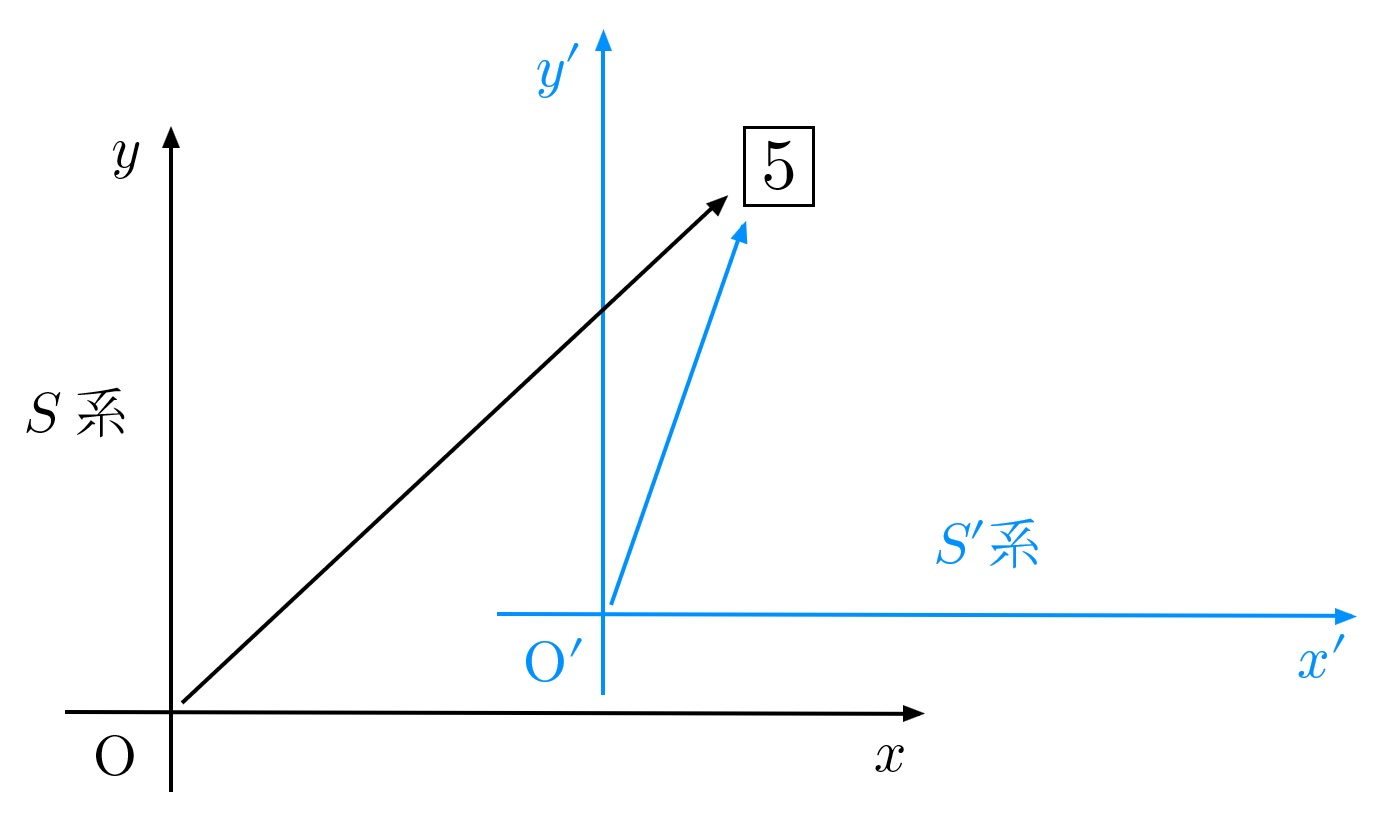
図3 スカラー量の説明。どちらの系から見ても、札には「5」と書かれている。
ようは、スカラーというのは、座標の取り方によらず、不変な量のことです。例えば、質量(不変質量)や電荷は、現代の物理学でも厳密にスカラー量です。
ベクトル
ベクトルと言っても色々ありますが、ここでは位置ベクトルを例に考えましょう。$S$ 系で位置ベクトル $\overrightarrow r = (x,y,z)$ にいる質点 $m$ が、$S'$ 系では位置ベクトル $\overrightarrow r' = (x',y',z')$ にいるとします。この状況を図に描いたのが下図4です。
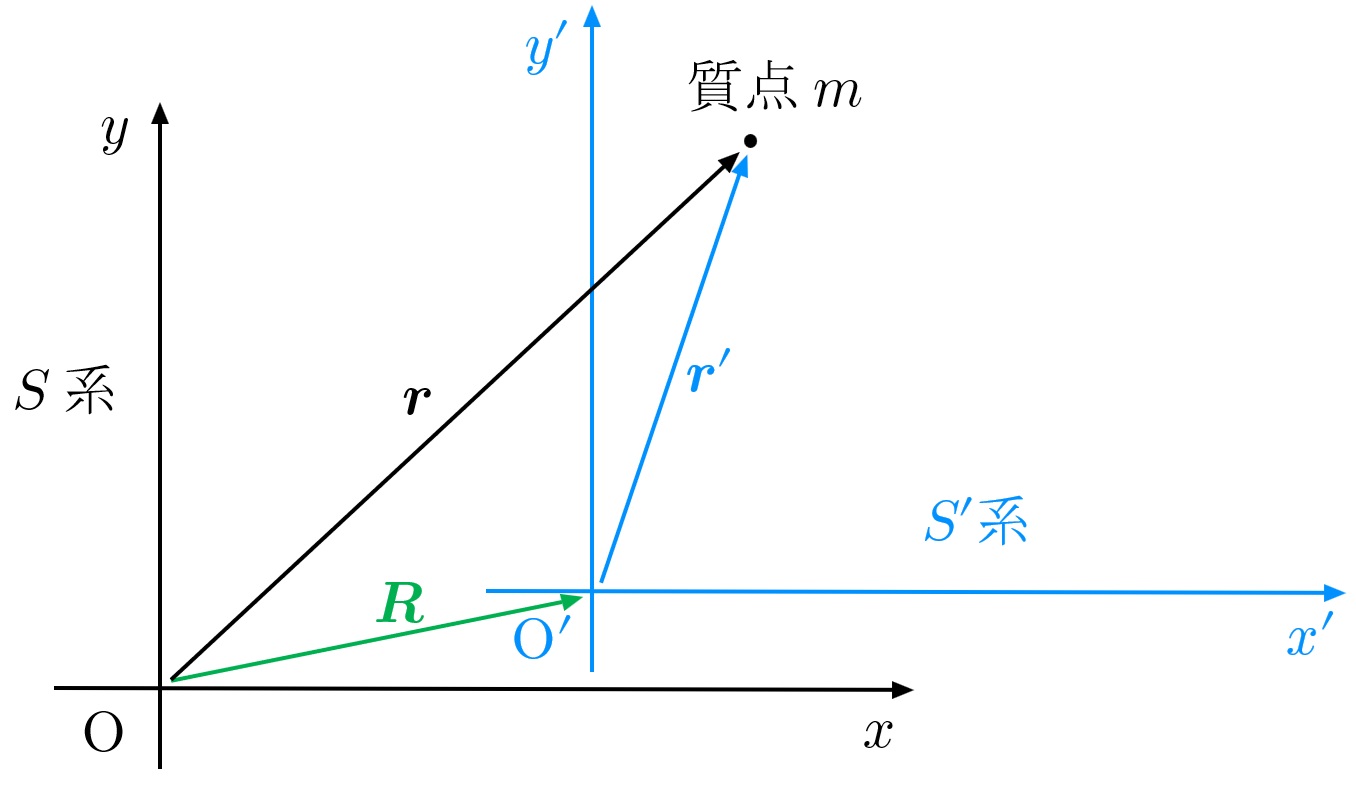
図4 ベクトル量の説明
$\overrightarrow r = (x,y,z)$ と $\overrightarrow r' = (x',y',z')$ はベクトルの成分がそれぞれ違います。違う座標なんだから、当たり前ですね。しかしこの「座標のずれ」を考慮することによって、$\overrightarrow r $ と $\overrightarrow r' $ の間に関係性をもたせることができます。
図のように、$S$ 系の原点 $\rm O$ 、$S'$ 系の原点 $\rm O'$ を用いて、ベクトル $\overrightarrow R $ を $\overrightarrow R = \overrightarrow{\rm{OO'}}$ と定義します。このとき、図からただちに \begin{align} \overrightarrow r = \overrightarrow R + \overrightarrow r' \end{align} が成り立ちます。このようにして、$\overrightarrow r $ と $\overrightarrow r' $ は異なるベクトルですが、座標系の関係性を適切に捉えることによって、2つのベクトルに関係性を持たせることができます。このような量のことを物理では特に、ベクトル量といいます。
ベクトルの種類
一口にベクトルと言っても、$2$ つの座標の変換に対する関係性に応じて、色々な種類があります。例えば、高校物理で習う速度 $\overrightarrow v $ と静電場 $\overrightarrow E $ は、座標変換に対して幾何ベクトル(高校で習うベクトル)と同じ変換則を持ちます。このようなベクトルは特に、反変ベクトルと呼ばれます。
一方で、相対性理論の文脈では、幾何ベクトルとは「逆の」変換則を持つようなベクトルもよく出てきて、共変ベクトルと呼ばれます。その他にも、磁束密度に代表されるような軸性ベクトルなどいろいろありますが、これらについて解説すると高校物理の範囲を大きく超えます。
