物質の電磁気学入門

1−1　モチベーション

本サイトでは、「真空中のMaxwell方程式は一通り知っているけど、誘電体中のMaxwell方程式はちんぷんかんぷん」という読者に、誘電体中のMaxwell方程式を説明する。

真空中のMaxwell方程式は、以下のように記述されることを思い出そう。

しかし、この方程式はこのままでは産業などには応用できない。我々が日常生きる世界に「真空」という状況はまずないからである。そこで、空気中や材質のような誘電体中で電磁場を扱う方程式を考えたくなる。

それでは、誘電体中では上の方程式は使えるだろうか。結論から言うと、全然使えない。

簡単な例

これについてみるために、誘電体中に点電荷$\, q\, $をおいたときを考えてみよう（以下、$\, q>0\, $とする）。イメージとしては、空気中（あるいは水中）に点電荷をひょいとおいたときを想像してみるとよい。簡単のため、誘電体は無限に広く境界がないものとする。

このとき、下図のように、点電荷$\, q\, $のまわりから電場$\, \boldsymbol E_0\, $が放射状に湧き出る。

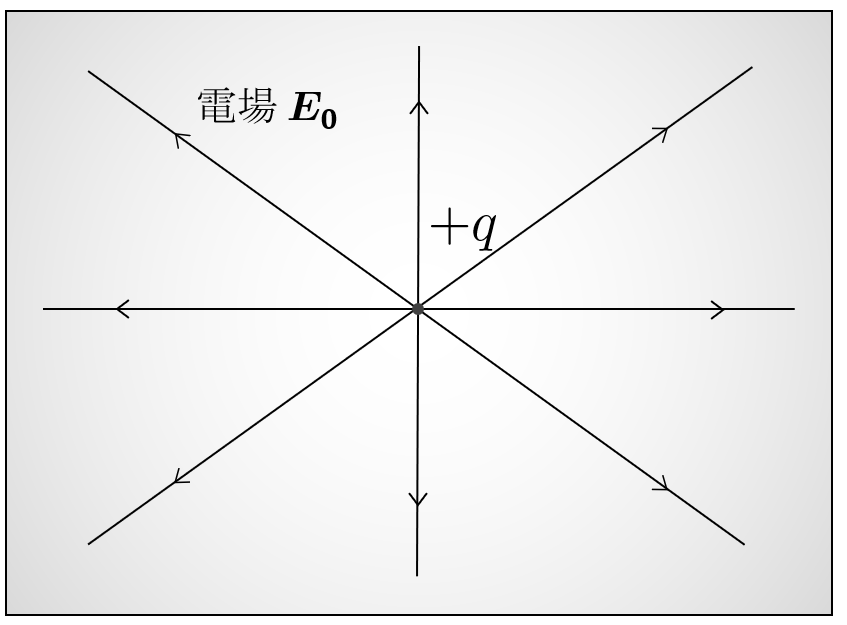
ここまでは真空中と同じである。ところが、誘電体中の場合は、真空中と異なり、誘電分極の現象が起きる。具体的には、点電荷$\, q\, $の周りにマイナスの分極電荷が生じ、その外側にマイナスの電荷を打ち消す分だけ、プラスの電荷が囲む。さらに、こうして生じた分極電荷は、新たに内向きの分極電場$\, \boldsymbol E_p\, $を生じる。これを図で書いたのが以下である。

このようにして、真空中では$\, \boldsymbol E_0\, $だった電場は、物質中では$\, \boldsymbol E_0 + \boldsymbol E_p\, $に弱められる。

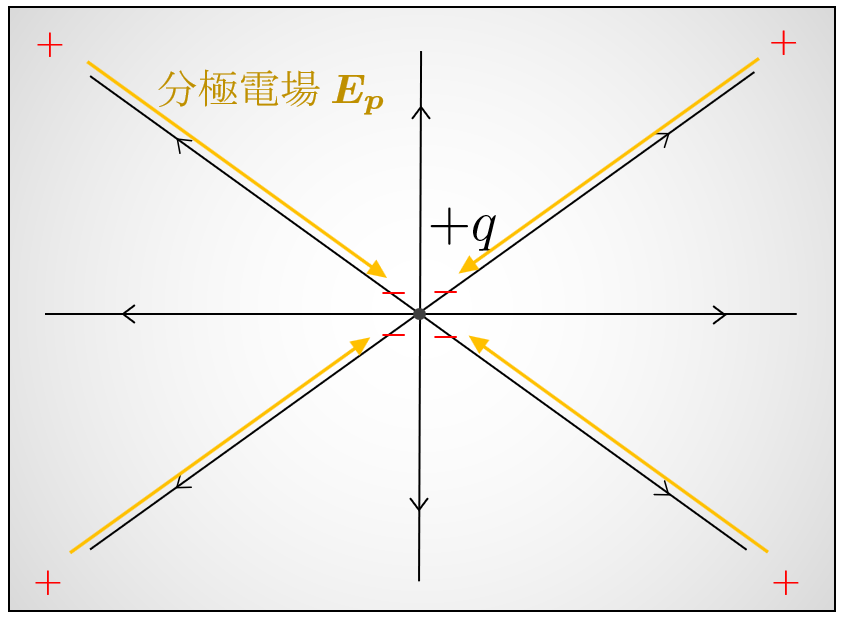
あるいは、より極端な例として、金属中に点電荷$\, q\, $をおいたときを考えてみよう。このとき、金属中では電子が自由に移動できることから、$\, q\, $のまわりには電荷がたちまち集まり、$\, q\, $が生じる電場をすべて遮蔽する（いわゆる静電遮蔽）。これは、上の例で$\, \boldsymbol E_p=-\boldsymbol E_0\, $となることに対応する。このように、一般に金属中では全電場$\, \boldsymbol E=0\, $が成り立つ。

このように考えると、真空中のGaussの法則 \begin{gather} \nabla \cdot \boldsymbol E_0(\boldsymbol r,t)=\frac{\rho(\boldsymbol r,t)}{\epsilon_0}\label{1.1} \end{gather} が、物資中では素朴に（つまり上の$\, \boldsymbol E_0\, $を$\, \boldsymbol E=\boldsymbol E_0+\boldsymbol E_p\, $に置き換えて）成り立たないことは、もはや明らかである。そしてこの原因は、上に述べたように静電遮蔽や誘電分極の効果により電荷$\, +q\, $がそのまわりにつくる電場が弱められたことに起因する。

誘電体中のGaussの法則

それでは、真空中のGaussの法則(\ref{1.1})が誘電体中でも成り立つためには、どのように方程式を修正すればよいだろうか。

言うまでもなく、誘電体中で真空中のGaussの法則が成り立たない原因は、誘電分極の効果によるものである。これが真空中のGaussの法則(\ref{1.1})にどのように影響するのか考えよう。誘電分極の結果生じる分極電荷分布を$\, \rho_p\, $とすると、これが生じる分極電場は$\, \boldsymbol E_p\, $なので、真空中のGaussの法則(\ref{1.1})より \begin{gather*} \nabla \cdot \boldsymbol E_p=\frac{\rho_p}{\epsilon_0} \end{gather*} が成り立つ（時空の引数は省略している）。次に、$\, \rho_p=-\nabla \cdot \boldsymbol P\, $となるようなベクトル$\, \boldsymbol P\, $を見つける。このようなベクトル$\, \boldsymbol P\, $は誘電分極と呼ばれる。誘電体が十分大きく境界が無視できるとき、このようなベクトル$\, \boldsymbol P\, $は確かに存在する（本ページ1ー4でのちに証明）。このとき、上の式はさらに \begin{gather*} \nabla \cdot (\epsilon_0\boldsymbol E_p +\boldsymbol P ) =0 \end{gather*} と変形される。 これをGaussの法則の式(\ref{1.1})と足し合わせて \begin{gather*} \nabla \cdot (\epsilon_0\boldsymbol E_0 +\epsilon_0\boldsymbol E_p +\boldsymbol P ) =\rho_{\rm{ext}} \end{gather*}

となる。なお、ここで電荷密度$\, \rho\, $を$\, \rho_{\rm{ext}}\, $に書き換えているのは、分極電荷$\, \rho_{p}\, $を含めず外部電荷だけを考えているというだけの意味である。$\boldsymbol E_0 +\boldsymbol E_p$が全電場なので、これを$\, \boldsymbol E\, $と書くことにして、結局、 \begin{gather*} \nabla \cdot (\epsilon_0\boldsymbol E +\boldsymbol P ) =\rho_{\rm{ext}} \end{gather*}

最後に、電束密度$\, \boldsymbol D=\epsilon_0\boldsymbol E +\boldsymbol P\, $を導入すると、物質中におけるGaussの法則が完成する。

以上が、物質中におけるGaussの法則の直感的な説明である。しかし、上の説明では誘電体に境界がある場合を考えておらず、誘電分極$\, \boldsymbol P\, $の物理的意味も明らかになっていない。本ページでは、より一般的な状況を考えながら、誘電分極$\, \boldsymbol P\, $が誘電体中における電気双極子モーメントの密度として物理的意味を持つことを示す。決して短くはないが、ベクトルを用いた電磁場解析の重要なところなので、がんばろう。

誘電体中のMaxwell方程式

結論だけをすべて書き下そう（もちろん、今はこれをすべて理解している必要はまったくない）。物質中では、以上の方程式は、以下のように書き換えられる。

\begin{gather} \nabla \cdot \boldsymbol D(\boldsymbol r,t)=\rho_{\rm ext}(\boldsymbol r,t) \label{5}\\ \nabla \cdot \boldsymbol B(\boldsymbol r,t)=\boldsymbol 0 \label{6}\\ \nabla \times \boldsymbol E(\boldsymbol r,t)=-\frac{\partial \boldsymbol B(\boldsymbol r,t)}{\partial t}\label{7}\\ \nabla \times \boldsymbol H(\boldsymbol r,t)=\frac{\partial \boldsymbol D(\boldsymbol r,t)}{\partial t}+\boldsymbol j_{\rm ext}(\boldsymbol r,t)\label{8} \end{gather}

上で電束密度$\, \boldsymbol D\, $、磁場$\, \boldsymbol H\, $は、以下のようにして新たに定義される。

\begin{gather*} \boldsymbol D(\boldsymbol r,t)=\epsilon_0 \boldsymbol E(\boldsymbol r,t)+\boldsymbol P(\boldsymbol r,t)\\ \boldsymbol B(\boldsymbol r,t)=\mu_0 \boldsymbol H(\boldsymbol r,t)+\boldsymbol M(\boldsymbol r,t) \end{gather*}

なお、$\, \boldsymbol P\, $は電気分極、$\, \boldsymbol M\, $は磁化である。

本ページでは、(\ref{5})式の導出と説明を行う。ここでは、電束密度$\, \boldsymbol D\, $、電気分極$\, \boldsymbol P\, $の物理的な意味が明らかにされる。これらにどのような物理的な意味があるのか、説明できるようになろう。

1−2　誘電体における電気的な分極

ここまででわかるように、誘電体中でのGaussの法則を考えるためには、誘電分極の現象をきちんと理解する必要がある。本節ではこれについて考えてみよう。

本節では、誘電分極が生じる微視的な描像を、無極性分子の代表である原子と極性分子（ただし強誘電体を除く）に分けて議論する。というのも、無極性分子（原子）と極性分子では、微視的なレベルでの電気的な性質がまったく異なるからである。ただし、以降の議論をみればわかるとおり、この2つは結果的にどちらも同じ結論を導くので、実際にMaxwell方程式を使用する場面では、これらの差異は気にしなくて良い。

次節では無極性分子について考察を行い、次々節で極性分子について考察する。

微視的な電気双極子1——無極性原子の場合

原子（無極性分子）に外から電場を書ける状況を考えよう。今回のように誘電体に外からかける電場は、分極電場と区別するため、外部電場と呼ばれる。外部電場$\,\boldsymbol E\,$を外部電場と強調するために$\,\boldsymbol E_{\rm{ext}}\,$と書くことも多いが、本節では簡単のためにたんに$\,\boldsymbol E\,$とかく。

このとき、分極後に原子が全体として中性であっても、正電荷と負電荷の中心がずれ、全体として電荷分布のばらつきが生じる。この描像で誘電分極を考えてみよう。

ここで、ある原子において、正電荷を$\, q\, $、負電荷を$\, -q\, $とし、正電荷の位置を始点として負電荷の位置を終点としたベクトルを$\,\boldsymbol d\,$と定める（図1参照）。このとき、外部電場を$\,\boldsymbol E\,$とすれば、$\,\boldsymbol d\,$と$\,\boldsymbol E\,$は同じ方向を向いている。

図1　電子の分極の概念図

ここで、この電荷分布のばらつきは外部電場によって生じたのだから、この分極によるエネルギーの変化は、$|\boldsymbol E|=E$、$|\boldsymbol d|=x\, $とすれば$\, -qEx\, $とかける。一方で、正電荷と負電荷の間には、互いに引き合おうとする復元力が生じる。イメージとしては、バネによる復元力と同じようなものだと考えればよい。この復元力は外部電場が弱いうちは$\, x\, $に比例することが知られているので、この復元力によるエネルギーの増加は$\, Kx^2/2\ (K>0)\, $とかける。以上から、分極にかかわる原子のエネルギー$\, U\, $は \begin{equation*} U=\frac{1}{2}Kx^2-qEx \end{equation*} である。このうち、エネルギー$\, U\, $が最小になるように実際の$\, x\, $は選ばれるので、これより、 \begin{equation*} x=\frac{qE}{K} \end{equation*} と定まる。以上から、$\, x\, $は$\, E\, $に比例するので、この原子の電気双極子モーメントを$\, \boldsymbol p=q\boldsymbol d\, $で定義すると、$\boldsymbol p\, $は定数$\, \alpha\, $を用いて

とかける。$\, \alpha\, $は物質によって異なる比例定数である。

微視的な電気双極子2——有極性分子の場合

次に有極性分子（但し強誘電体は除く）を考えよう。先述の通り、有極性分子でも電気双極子モーメント$\, \boldsymbol p\, $と外部電場$\, \boldsymbol E\, $が比例関係にあるという結果は先ほどの無極性分子と同じだが、微視的なレベルでの様相は、無極性分子のそれとは大きく異なる。

有極性分子では、分子一つ一つが最初から電気双極子モーメント$\, \boldsymbol p\, $を持っている。これは外部電場$\, \boldsymbol E\, $の影響に関係なく存在し、熱運動をしているはずである。簡単のため電気双極子モーメント同士の相互作用は無視しよう。

直感的には外部電場がないとき、分子の熱運動によって電気双極子モーメント$\, \boldsymbol p\, $はバラバラであり、平均すると0である（つまり分極は生じていない）と思われる。ところが、外部電場があると、$\, \boldsymbol p\, $は電場$\, \boldsymbol E\, $と同じ方向を向いているほうがエネルギー的に安定だろう。

それでは、このような分子の熱運動は、どう定量的に扱えばよいのだろうか。まず、外部電場$\, \boldsymbol E\, $に垂直な方向の分極は巨視的にみれば統計的にほぼ$\, 0\, $とみなせるだろうから、我々は外部電場$\, \boldsymbol E\, $と同じ方向の分極のみを考えればよい。そこで、外部電場方向の分極の平均を求めたいのだが、ここはまさに統計力学——マクロとミクロをつなぐ力学——の出番である。ある分極$\, \boldsymbol p\, $をもつ双極子のエネルギーは$\, -\boldsymbol p\cdot \boldsymbol E=-pE\cos\theta\, $とかける（ここで$\, \theta\, $は$\, \boldsymbol p\, $と$\, \boldsymbol E\, $のなす角である）。これより、その双極子$\, 1\, $個当たりの分配関数$\, z(\beta)\, $は、古典的に \begin{equation} z(\beta)=\int_0^\pi d\theta \int_0^{2\pi }d\phi \, e^{\beta pE\cos\theta}\sin\theta\label{p03} \end{equation} である。これは積分実行できて、 \begin{equation} z(\beta)=\frac{4\pi}{\beta p E}\sinh(\beta p E)\label{p04} \end{equation} となる。とくに、高温$\, \beta pE\ll 1\, $のとき、(\ref{p04})式は、 \begin{equation} z(\beta)\approx 4\pi\label{p05} \end{equation} とかける。

また、外部電場方向の分極$\, p\cos\theta\, $の期待値$\, \langle p\cos\theta \rangle\, $は

である。ここで、新たにランジュバン関数$\, L(x)\, $を \begin{equation} L(x)=\coth x-\frac{1}{x}\label{p07} \end{equation} と定義すると、$\, \langle p\cos\theta \rangle\, $の表式は、 \begin{equation*} \langle p\cos\theta \rangle=pL(\beta p E) \end{equation*} と簡単な形で書くことができる。

$\, L(x)\, $の概形について考察しよう。まず、$\, x\to\pm \infty\, $のとき、$\, L(x)\, $は \begin{equation} L(x) \to \pm 1\label{p08} \end{equation} に漸近する。今回は$\, x=\beta p E\, $とおいているので、これは低温かつ電場が十分に強いときに、電場双極子がほとんど電場と同じ方向を向いていることを示している。これは我々の直観に合っている。

次に、高温かつ電場が十分小さいとき（$\, x=\beta p E\ll 1\, $）を考えてみよう。我々が日常的になじみがあるのは、たいていこのような場合である。このとき、我々はランジュバン関数$\, L(x)=\coth x-1/x\, $を$\, x=0\, $のまわりで展開する必要がある。これは特異点の周りの積分なので、数学的にはローラン展開を考える必要がある。

まず、$\, L(x)\, $は \begin{equation} L(x) =\frac{e^{2x}+1}{e^{2x}-1}-\frac{1}{x}\label{p09} \end{equation} と書き直せる。これより、$\, \dfrac{1}{e^{2x}-1}\, $をローラン展開すれば問題は解決する。これは初歩的な 物理数学の問題であるが、今回は教育的な視点から、少し違ったアプローチから解説してみよう。

次のような展開を考えてみる。 \begin{equation} \frac{x}{e^x-1} =\sum_{n=0}^\infty \frac{B_n}{n!}x^n\label{p10} \end{equation} 　ここで係数$\, B_n\, $はベルヌーイ数と呼ばれる。ベルヌーイ数と言われると少し難しい感じがするかもしれないが、$\, B_n\, $を始めからいくつか求めるのは簡単である。それは、(\ref{p10})を

と書き換え、各$\, x^n\, $の係数を比べればよい。これによって、ベルヌーイ数が、 \begin{equation} B_0=1,\ B_1=-\frac{1}{2},\ B_2=\frac{1}{6},\ \cdots \end{equation} と求まる。今回はこの程度まで求めれば十分である。これを再び(\ref{p10})に代入し、$\, x\to 2x\, $とおきかえることによって、我々は、求めたいローラン展開を得ることができる。

あとは、(\ref{p09})に(\ref{p12})の結果を代入して、展開して整理すればよい。すると、$\, 1/x\, $の項はうまく消えて、結局 \begin{equation} L(x)=\frac{x}{3}+O(x^3)\qquad (x\ll 1) \end{equation} が求まる。これによって、$\, x=\beta p E\ll 1\, $のとき、$\, \langle p\cos\theta \rangle\, $は、

と求めることができる。

実のところ、(\ref{p13})式の結果は、(\ref{p06})式に議論を巻き戻すによって、簡単に求めることができる。最後に、これについても確認しておこう。高温では$\, \beta pE\ll 1\, $とみなせるので、$\, e^{\beta pE\cos\theta}\approx 1+\beta pE\cos\theta\, $と近似してしまえばよくて、これより、(\ref{p06})式は

となる。

以上の結果をまとめよう。我々が日常的に問題にする高温かつ低電場、すなわち$\, \beta pE\ll 1\, $のとき、やはり分極の期待値$\, \langle p\cos\theta \rangle\, $は電場に比例し、(\ref{p1})式と同様に

が成立する。$\, \alpha\, $は物質によって異なる比例定数である。なお、実際の場面では、(\ref{p1})、(\ref{p2})式の右辺の$\, \boldsymbol E\, $は、外部からかけられる電場ではなく、回りの双極子の分極の影響も含めた、誘電体内の全電場のことを考えなくてはならない。

まとめ

前の2項では無極性分子、有極性分子それぞれについて簡単な模型を考え、一様な外部電場$\, \boldsymbol E\, $中ではこれらの分子が外部電場$\, \boldsymbol E\, $に比例する電気双極子としてふるまうことが確認できた（(\ref{p1})、(\ref{p2})式）。実際に、この比例関係は弱い電場中であればほとんどの物質について成り立つ関係であることがよく知られている。なお、(\ref{p1})、(\ref{p2})式における比例定数$\, \alpha\, $は分極率と呼ばれる。くり返し述べたように分極率の値は物質によって異なる。

1−3　電位の多重極展開

ところで、今後の議論の準備として、電位の多重極展開についておさらいしておこう。電位の多重極展開は真空の電磁気学で学習済みかもしれないが、忘れている読者のために、もう一度初歩から復習しておく。

Legendre多項式

Legendre多項式$\, P_n(x)\, $は、母関数を用いて以下のように定義される関数である。 \begin{equation} \frac{1}{\sqrt{t^2-2xt+1}}=\sum_{n=0}^\infty P_n(x)t^n\label{legendre} \end{equation} 　このLegendre多項式の性質はすでに数学者によってよく調べられており、上記の他にも、ロドリゲスの公式や微分方程式など、様々な定義が可能である。ただし今回はそのような数学的な事実には深入りしないことにする（そして、今回はその必要はない）。

(\ref{legendre})式を見つめて我々が気付くのは、ルジャンドル多項式は母関数をTaylor展開すれば、手計算でもいくつか具体的に求められるということである。実際、この方法なら母関数さえ暗記していれば、Legendre多項式をわざわざ覚えていなくても、その場で計算で求めることができる。そこで、母関数を \begin{equation*} f(t)=(t^2-2xt+1)^{-\frac{1}{2}} \end{equation*} とおいていくらか微分してみると、

となるので、これより、 \begin{equation*} f(0)=1,\quad f'(0)=x,\quad f''(0)=3x^2-1 \end{equation*} となり、以上より、 \begin{equation*} P_0(x)=1,\quad P_1(x)=x,\quad P_2(x)=\frac{1}{2}(3x^2-1) \end{equation*} を得る。今回の多重極展開への応用では、この程度まで求めれば十分である。

電荷分布と多重極モーメント

位置ベクトル$\, \boldsymbol r'\, $において電荷密度$\, \rho(\boldsymbol r')\, $で表される電荷が、十分遠方の位置$\, \boldsymbol r\, $にもたらす電位$\, \phi(\boldsymbol r)\, $について考えてみよう。まず、電位$\, \phi(\boldsymbol r)\, $は \begin{equation} \phi(\boldsymbol r)=\frac{1}{4\pi \epsilon_0}\int\frac{\rho(\boldsymbol r')}{|\boldsymbol r-\boldsymbol r'|}d^3\boldsymbol r'\label{1.3} \end{equation} と表される。するとこのとき、前節のLegendre多項式のTaylor展開により、$|\boldsymbol r|=r,|\boldsymbol r'|=r'$、$\boldsymbol r\, $と$\, \boldsymbol r'\, $のなす角を$\, \theta\, $とすれば、

とかける。ただし$\, r'/r\ll 1\, $であるから、$\, r'/r\, $の$\, 3 \, $次以上の項は十分小さいものと見なして省略した。これをもとの(\ref{1.3})式に代入すれば、

となる。第2項は

とかけるので、電気双極子モーメント$\, \boldsymbol p\, $を

とおけば、 \begin{equation} \frac{1}{4\pi \epsilon_0 r^3}\int rr'\cos\theta d^3\boldsymbol r=\frac{\boldsymbol r\cdot\boldsymbol p}{4\pi \epsilon_0 r^3}\label{1.6} \end{equation} とまとめることができる。第3項ついては、電気4重極子モーメント$\, Q_{ij}\, $を

とおけば、

とかける。

以上(\ref{1.6})、(\ref{1.8})を(\ref{1.4})に代入して、

となる。(\ref{1.9})式のうち、第1項は正味の電荷が$\, \boldsymbol r\, $にもたらす電位であり、第2項は電気双極子モーメント$\, \boldsymbol p\, $が$\, \boldsymbol r\, $にもたらす電位であり、第3項は電気四重極子モーメント$\, Q_{ij}\, $が$\, \boldsymbol r\, $にもたらす電位と考えることができる。

電気双極子モーメントについて

ここまでの議論から推測がつくように、物質中の静磁場の法則においては、電気双極子モーメント$\, \boldsymbol p\, $が重要な手掛かりとなる。それでは、電気双極子モーメントとはいったいどのような概念なのだろうか。これについて説明をしておく必要があるだろう。

まず確認しておく必要があるのは、一般に電気双極子モーメント$\, \boldsymbol p\, $は位置を持っているということである。ただ、おのおのの電気双極子を作り出している原子や分子が位置を持っているのだから、これは考えてみれば当たり前なことである。電荷が位置をもつように、電気双極子モーメントも、それが置かれる場所として、位置を持っていなければならないのである。

また、今回の議論における電気双極子モーメント$\, \boldsymbol p\, $は、誘電体中の微視的な原子や分子における分極を想定しているものだから、それらが持つ電気双極子モーメントは原子や分子レベルの小さなものであり、その数も多い。それゆえ、それら電気双極子モーメントに1つ1つに番号をつけて \begin{equation*} \boldsymbol p_1,\ \boldsymbol p_2,\ \cdots ,\ \boldsymbol p_n \end{equation*} と名付けることができるはずだ。もちろん、それぞれの双極子$\, \boldsymbol p_i\, $は双極子ごとに固有の位置があるので、これらを$\, \boldsymbol r_i\, $としよう。

以上の考えを踏まえると、位置ベクトル$\, \boldsymbol r'\, $に電荷$\, q\, $が存在するとき、電荷密度が$\, \rho(\boldsymbol r)=q\delta(\boldsymbol r-\boldsymbol r')\, $と書かれるのと同じようにして、電気双極子モーメント$\, \boldsymbol p_i\, $の密度$\, \boldsymbol P'(\boldsymbol r)\, $は \begin{equation*} \boldsymbol P'(\boldsymbol r)=\sum_i \boldsymbol p_i\delta(\boldsymbol r-\boldsymbol r_i) \end{equation*} と書ける。もちろんこれは間違いではない。ただ、我々は誘電体に関する巨視的な議論をしたいので、わざわざ$\, \boldsymbol p_i\, $をDiracのデルタ関数を用いてすべて「列挙」し、全部足し上げるのは現実的な議論ではない。むしろ我々が知りたいのは、トゲトゲになっている不自然な状態の密度$\, \boldsymbol P'(\boldsymbol r) \, $を平均して「ならし」、連続的で有限な（本当の意味での）「密度」にすることである。そこで、位置ベクトル$\, \boldsymbol r\, $に存在するある小さな空間$\, V_{\boldsymbol r}\, $内において$\, \boldsymbol P'(\boldsymbol r)\, $を積分し、その値を体積$\, V\, $で割った値

を考えれば、$\, \boldsymbol P(\boldsymbol r)\, $は$\, V_{\boldsymbol r}\, $内において$\, \boldsymbol P'(\boldsymbol r)\, $をならした、本当に巨視的な意味での「密度」となっている。この$\, \boldsymbol P(\boldsymbol r)\, $を電気分極といい、今後物質中の電磁場を考える際に非常に重要な概念である。

さいごに、以上の$\, \boldsymbol P'(\boldsymbol r)\, $を「ならす」考えの妥当性について述べておこう。(\ref{1.10})式のような平均化の議論は、$\, V_{\boldsymbol r}\, $内において$\, \boldsymbol p_i\, $の数が統計的に十分多くないとできない議論である。というのも、$\, V_{\boldsymbol r}\, $内における$\, \boldsymbol p_i\, $の数があまりにも少なすぎると、統計的に$\, \boldsymbol P(\boldsymbol r)\, $の値が信用できなくなってしまうからである。この「ならし」の技術の信用性は、この$\, V_{\boldsymbol r}\, $のとりうる大きさと、その中にある$\, \boldsymbol p_i\, $の数にかかっている。ところが、先述のように$\, \boldsymbol p_i\, $は原子や分子レベルで生じたものであり、その個数密度は極めて多い。実際、$\, V_{\boldsymbol r}\, $として一辺$\, \boldsymbol 1\mu m\, $の立方体上の大きさをとったとしても、これは原子・分子レベルでは十分広い大きさである。このように考えれれば、(\ref{1.10})式の電気分極の考えは、微視的なレベルからみても、十分に妥当性を持っていることがわかる。

真空中に電気双極子を置く場合の注意

我々はまず電気分極を(\ref{1.10})によって定義したが、これは誘電体の内部やその境界についても巨視的な——ならした——議論ができることを示すためである。一方で、たとえば我々が電磁気学の演習問題を解くときには、真空中に（大きさの無視できる）電気双極子モーメントを置くような場面に遭遇することが、よくある。このような問題を解くためには、むしろデルタ関数の表式を残しておいて、

を用いるほうがむしろ便利である。

ここまでで(\ref{1.10}),(\ref{1.10a})という2つの電気分極の定義が登場しているが、いずれの定義も物理的に本質的な意味はまったく同じであることは、読者にはもう明らかであると思う。あとは、状況に合わせて、使いやすい方の定義を柔軟に用いればよいのである。

1−4　誘電体中のGaussの法則の導出

電気分極で電位を表す

(\ref{1.9})式の第2項は、1個の磁気モーメント$\, \boldsymbol p_i\, $がつくる微視的なスケールのものに過ぎないので、電気分極$\, \boldsymbol P(\boldsymbol r)\, $を用いて、巨視的なものに書き換えよう。位置ベクトル$\, \boldsymbol r'\, $にある微小体積$\, d^3\boldsymbol r'\, $における分極は$\, \boldsymbol P(\boldsymbol r')d^3\boldsymbol r\, $である。電気分極といっても、それは電気双極子モーメント$\, \boldsymbol p_i\, $がたくさん足されたものを単位体積当たりで表したものにすぎないから、$\, \boldsymbol P(\boldsymbol r')d^3\boldsymbol r'\, $が位置$\, \boldsymbol r\, $にもたらす電位は、(\ref{1.9})式の第2項より、 \begin{equation*} \frac{1}{4\pi \epsilon_0}\frac{\boldsymbol P(\boldsymbol r')d^3\boldsymbol r'\cdot(\boldsymbol r-\boldsymbol r')}{|\boldsymbol r-\boldsymbol r'|^3} \end{equation*} とかける。これを集めて積分することにより、電気分極$\, \boldsymbol P(\boldsymbol r')\, $が位置$\, \boldsymbol r\, $にもたらす電位$\, \phi_P(\boldsymbol r)\, $は、

である。

ここで少し数学的なトリックを使ってみよう。以下の数式を利用することを考える。 \begin{equation*} \nabla' \left(\frac{1}{|\boldsymbol r-\boldsymbol r'|}\right)=\frac{\boldsymbol r-\boldsymbol r'}{|\boldsymbol r-\boldsymbol r'|^3} \end{equation*} ただしここで、$\nabla'$にプライムがついているのは、$\, \boldsymbol r\, $ではなく$\, \boldsymbol r'\, $の座標について演算を行うことを示している。このとき、(\ref{1.11})式は

と計算できる。上の式において積分区間は全空間を想定しているが、誘電体の外ではもちろん$\, \boldsymbol P(\boldsymbol r)\, $は0なので、積分区間は誘電体の内部に絞ってよい。そこで、誘電体の全表面を$\, S_P$、その内部を$\, V_P\, $とすれば、上の式は

とかける。(\ref{1.12})式は、誘電分極$\, \boldsymbol P(\boldsymbol r)\, $がつくる電位$\, \phi_P(\boldsymbol r)\, $が、誘電体の内部電荷密度$\, \rho_P\, $と、表面電荷密度$\, \sigma_P\, $

がつくる電位に等しいことを示している。これはまさに誘電体が作る誘電分極の現象そのものである。我々は着実に核心に迫っている。

誘電体中のGaussの法則

上の$\, \rho_P\, $、$\, \sigma_P\, $は、誘電体が作る電気分極$\, \boldsymbol P\, $が作る電場と同じ電場を作る電荷分布を指す。そこで、これらに真空中のGaussの法則 \begin{equation} \int_S \epsilon_0\boldsymbol E(\boldsymbol r)\cdot\boldsymbol n(\boldsymbol r)dS=\int_V\rho(\boldsymbol r)d^3\boldsymbol r\label{gauss} \end{equation} を適用することを考えよう。これより、$\rho_P$、$\, \sigma_P\, $（つまり$\, \boldsymbol P(\boldsymbol r)\, $）に由来する電場を$\, \boldsymbol E(\boldsymbol r)\, $とおけば、

が成立する。$\, S\, $は任意の閉曲面であり、$\, S_P\, $は$\, S\, $内の誘電体の表面である。また、$\, V_P\, $は$\, S\, $内の誘電体の内部である。

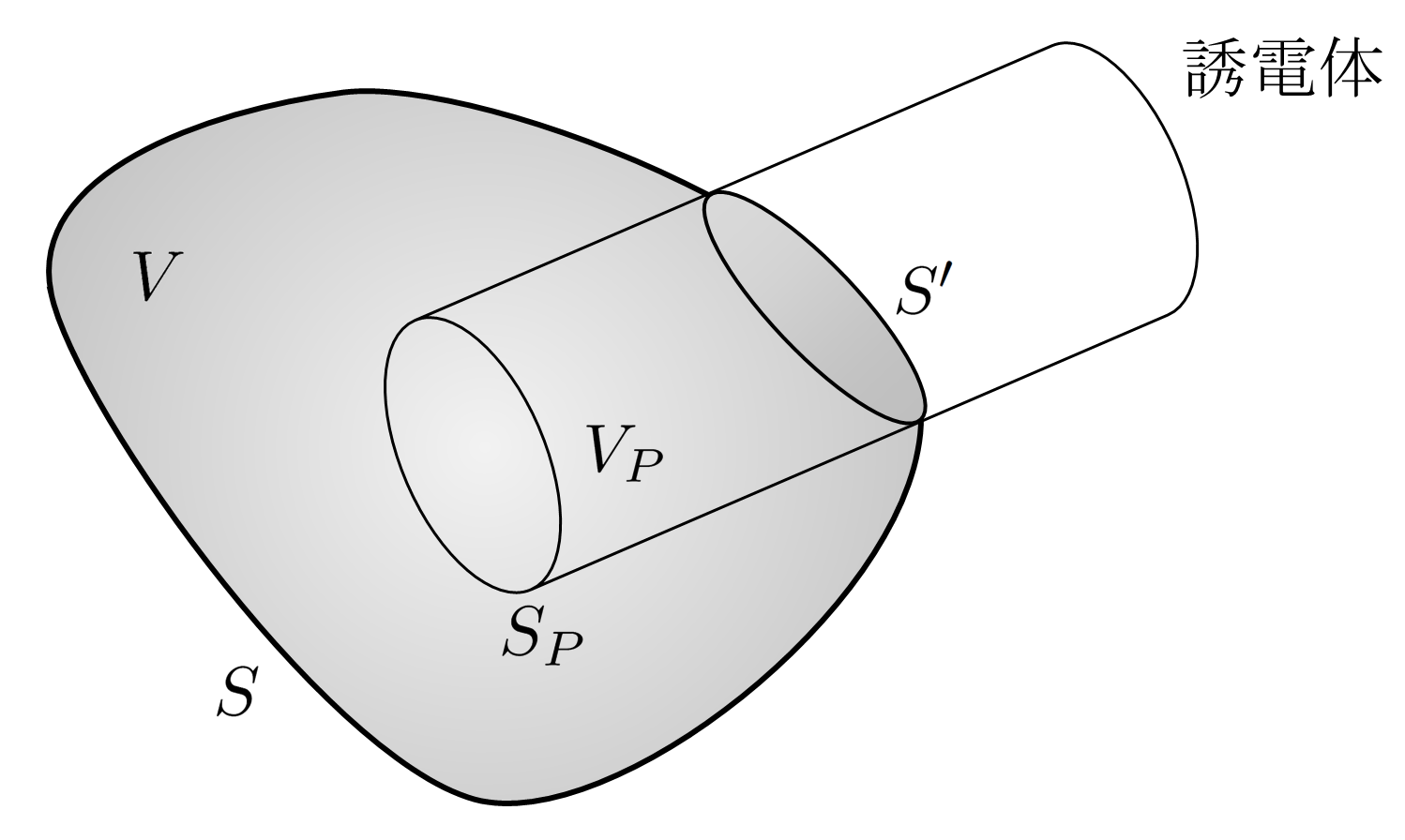
図2　誘電体のガウスの法則を考える閉曲面

このとき、(\ref{1.13})式の右辺第1項は、$\, \rho_P=-\nabla\cdot \boldsymbol P(\boldsymbol r)\, $であることより、ガウスの定理を適用できて、

となる。これを(\ref{1.13})式に代入しなおせば、$\, S_P\, $に関する積分がキャンセルして

となる。右辺の積分範囲は$\, S'\, $のみとなっているが、これは$\, S\, $全体に拡張してもよいので、以上より、 \begin{equation*} \int_S \big\{\epsilon_0\boldsymbol E_P(\boldsymbol r)+\boldsymbol P(\boldsymbol r)\big\}\cdot\boldsymbol n(\boldsymbol r)dS=0 \end{equation*} となる。これに、真電荷が作る真空中ののGauss法則(\ref{gauss})を足し合わせれば、

となる。もちろん、右辺の$\, \rho(\boldsymbol r)\, $は$\, S\, $内にある真電荷の密度である。以上から、電束密度$\, \boldsymbol D(\boldsymbol r)\, $を

とおけば、我々は、誘電体中のGaussの法則

を得ることができる。もちろん、微分形は

である。

電束密度について

新たな概念が登場してきたとき、その概念が一体物理的にどのような意味を持つのか、捉えておかなくてはならない。ここで出てきた電束密度$\, \boldsymbol D(\boldsymbol r)\, $とはいったいどのような概念なのか説明しておく必要があるだろう。まず、真空中では$\, \boldsymbol P(\boldsymbol r)=0\, $なので \begin{equation*} \boldsymbol D(\boldsymbol r)=\epsilon_0\boldsymbol E(\boldsymbol r) \end{equation*} である。また、(\ref{p1})、(\ref{p2})式のように電気双極子モーメントが電場$\, \boldsymbol E\, $に比例するような誘電体では、分極$\, \boldsymbol P\, $が$\, \boldsymbol E\, $に比例するために、比例定数を$\, \epsilon_0\chi\, $として

と書くことができる。これより、電束密度は

となるので、$\, \epsilon_0(1+\chi)=\epsilon\, $とおけば、

と書くことができる。このような性質を持つ誘電体を常誘電体と呼ぶ。$\, \epsilon\, $の値は常誘電体の種類によって異なる。一方で、誘電体によっては、電場$\, \boldsymbol E\, $が無くても分極$\, \boldsymbol P\, $をもつような物質も存在する。このような誘電体を強誘電体と呼ぶ。他にも、外部から圧力を加えると電気的に分極する圧電体など、様々な誘電体が存在する。

$ {\color[RGB]{30,120,200}\boldsymbol p}\, $が作る電場$\, \boldsymbol E$

さいごに、原点にある電気双極子モーメント$\, \boldsymbol p\, $がそのまわりに作る電場$\, \boldsymbol E_p(\boldsymbol r)\, $を導出しておこう。とはいえ、$\, \boldsymbol E_p(\boldsymbol r)\, $は、(\ref{1.9})式の第2項 \begin{equation*} \phi_p=\frac{\boldsymbol r\cdot\boldsymbol p}{4\pi \epsilon_0 r^3} \end{equation*} において、$\, \boldsymbol E_p(\boldsymbol r)=-\nabla \phi_p\, $を計算するだけである。これを行うと、

と計算できる。なお、上の式において$\, \nabla(\boldsymbol r\cdot\boldsymbol p)\, $の$\, i\, $成分は$\, \partial_ir_jp_j\, $とかける。$\, p_j\, $は定数であり、$\, \partial_ir_j=\delta_{ij}\, $なので、これより$\, \nabla(\boldsymbol r\cdot\boldsymbol p)=\boldsymbol p\, $。

以上より、電気双極子の位置を原点から$\, \boldsymbol r'\, $にずらせば、位置$\, \boldsymbol r'\, $にある電気双極子$\, \boldsymbol p\, $が位置$\, \boldsymbol r\, $に作る電場は

である。

<%-- $$ x = \frac{ \color[RGB]{30,120,200}-b \color[RGB]{0,0,0} \pm \sqrt{b^2 - 4ac}}{2a} $$ --%>