物質の電磁気学入門

Electromagnetism of Matter

第3式、第4式（変動電磁場）

3−1　物質中におけるFaradayの法則の導出

真空中におけるMaxwell方程式の第3式は，Faradayの法則 \begin{equation} \nabla\times \boldsymbol E(\boldsymbol r,t)=-\frac{\partial \boldsymbol B(\boldsymbol r,t)}{\partial t}\label{3.1} \end{equation} であった。この式が誘電体中でどのように書き換えられるか考えよう。

右辺の検討

それでは(\ref{3.1})の右辺がどう修正されるのか検討しよう。最もありうる右辺の変更は、磁束密度$\, \boldsymbol B\, $が磁場$\, \boldsymbol H\, $へと置き換えられることである。しかし結論から述べると、このような変更は物理的にありえない。これは次のように考えることで理論的に要請される。まず、(\ref{3.1})式を積分形に直すと，次のようになる。

\begin{equation} \int_C \boldsymbol E(\boldsymbol r,t)\cdot d\boldsymbol \ell=-\frac{\partial }{\partial t}\int_S\boldsymbol B(\boldsymbol r,t)\cdot \boldsymbol n dS\label{3.2} \end{equation}

ここで$C$は任意の線ループであり，$\, S\, $はその線ループが作る面である（下図）。

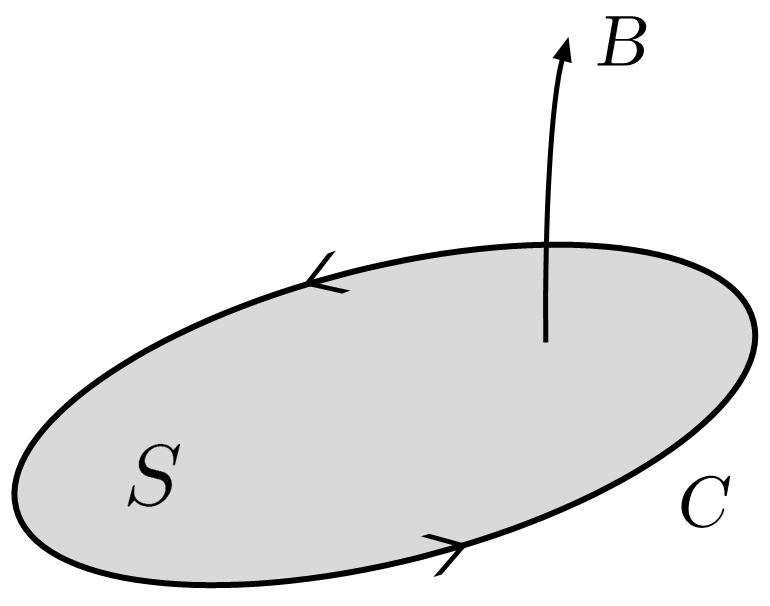
ここでポイントとなるのは，面$\, S\, $はその境界が$\, C\, $であれば，どのような形状の面をとっても構わないということである。これは次のようにして示される。下図のように，同じループ$\, C\, $を境界とする逆向きの突起を持った面$\, S_1,S_2\, $を用意しよう。

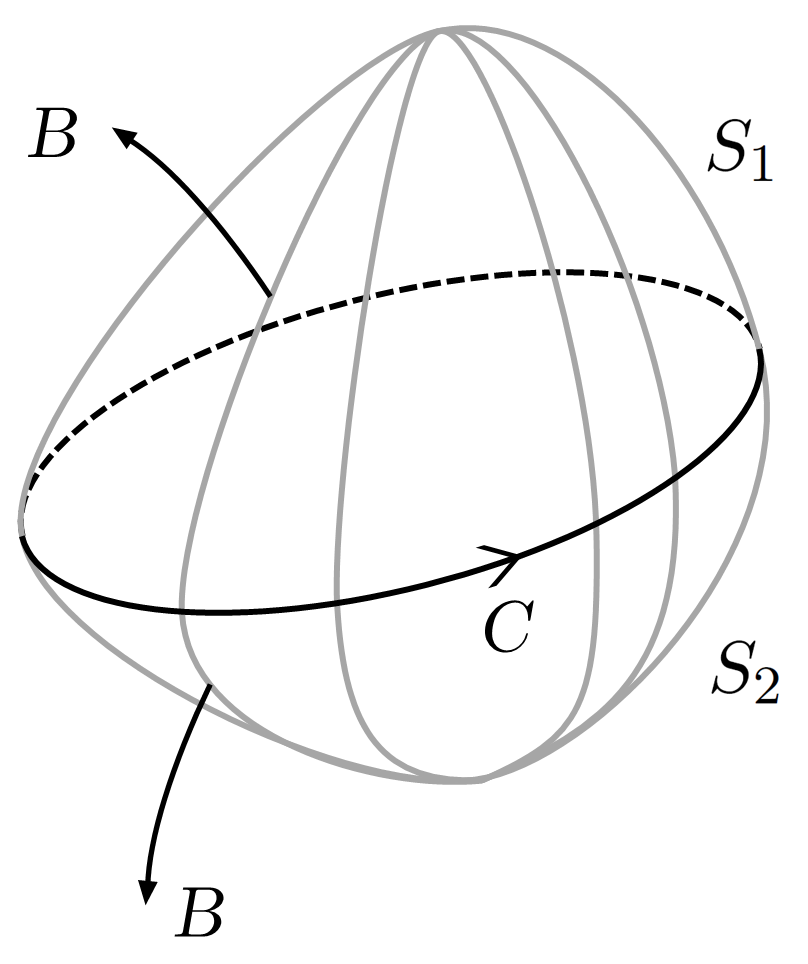
するとこのとき，$\, S_1\, $と$\, S_2\, $を合わせた面$\, S_1+S_2\, $は閉曲面となるので，磁束密度に関するガウスの法則を適用すれば， \begin{equation*} \int_{S_1+S_2}\boldsymbol B\cdot \boldsymbol ndS=0 \end{equation*} となる。ただし面ベクトル$\, \boldsymbol n\, $はすべて外向きに取ったことに注意する。これより，それぞれの面積分は，同じ値となる。 \begin{equation} \int_{S_1}\boldsymbol B\cdot \boldsymbol n_1dS=\int_{S_1}\boldsymbol B\cdot \boldsymbol n_2dS\label{3.3} \end{equation} ここで$\, \boldsymbol n_1\, $と$\, \boldsymbol n_2\, $は，ループ$\, C\, $からみてすべて単一の方向になるように置いていることに注意する。このように考えることで，(\ref{3.2})の右辺の積分は，閉曲面$\, S\, $の境界が$\, C\, $とつながっていれば，その形状によらないことが確認できる。

このとき，もし物質中において，$\, S_1\, $を透磁率$\, \mu_1\, $の磁性体，$\, S_2\, $を透磁率$\, \mu_2\, $の磁性体が占めていたとしよう。するとこのとき，もし(\ref{3.3})の積分の中身が$\, \boldsymbol B\, $ではなく$\, \boldsymbol H\, $となってしまった場合，(\ref{3.3})の等号はちゃんと同じになるだろうか。

もちろんこれは， \begin{equation*} \boldsymbol B_1=\mu_1 \boldsymbol H_1,\quad \boldsymbol B_2=\mu_2 \boldsymbol H_2 \end{equation*} と書けることを考えれば，明らかに成り立たない。このように考えれば，(\ref{3.1})式の右辺を書き換える必要性は，どうやらなさそうである。

左辺の検討

次に(\ref{3.1})式の左辺を検討しよう。最もありうる左辺の変更は、電場$\, \boldsymbol E\, $の電束密度$\, \boldsymbol D\, $への置き換えである。これを考察するためには、考えている誘電体における誘電分極$\, \boldsymbol P\, $が、どのように(\ref{3.1})式に影響するのか考える必要がある。

いま、考えている誘電体に誘電分極$\, \boldsymbol P\, $が生じているとしよう。このとき、この誘電分極は、誘電体の内部電荷密度$\, \rho_P\, $、および表面電荷密度$\, \sigma_P\, $

\begin{equation} \rho_P=-\nabla\cdot \boldsymbol P(\boldsymbol r),\quad \sigma_P=\boldsymbol P(\boldsymbol r)\cdot \boldsymbol n(\boldsymbol r')\label{prho} \end{equation}

を生じる。

実のところ、誘電分極$\, \boldsymbol P\, $が誘電体にもたらす影響は、これだけではない。誘電分極$\, \boldsymbol P\, $が時間的に変動している場合は、誘電体の分極電荷密度は時間的に変化する。これはまさに電流である。この電流は、後に示すように、(\ref{cc})式

\begin{equation*} \boldsymbol j_P(\boldsymbol r,t)=\frac{\partial \boldsymbol P(\boldsymbol r,t)}{\partial t} \end{equation*}

によりかける（説明がくどくなるので、証明は後回しにする）。

以上で述べた$\, \rho_P,\ \sigma_P,\ \boldsymbol j_P \, $が(\ref{3.1})式にどのような変化をもたらすか考えればよい。しかし実のところ、(\ref{3.1})式には電荷密度、および電流密度に依存する式はなく、(\ref{3.1})式に代入する部分はない。これより、誘電分極の効果による(\ref{3.1})式の変更はない。

以上の議論により，

\begin{align} \nabla\times \boldsymbol E(\boldsymbol r,t)=-\frac{\partial \boldsymbol B(\boldsymbol r,t)}{\partial t}\label{3.4} \end{align}

は，物質中でも正しく成立する。

なお、これまでの議論は、誘電分極$\, \boldsymbol P(\boldsymbol r)\, $だけでなく、磁化$\, \boldsymbol M(\boldsymbol r)\, $に対しても同様に適用できることに注意しよう。磁化$\, \boldsymbol M(\boldsymbol r)\, $がつくる磁束密度は，その磁性体の内部を流れる体積電流密度$\, \boldsymbol j_M\, $と，表面を流れる表面電流密度$\, \boldsymbol i_M\, $ \begin{equation*} \boldsymbol j_M=\nabla\times \boldsymbol M ,\quad \boldsymbol i_M=-\boldsymbol n\times \boldsymbol M \end{equation*} に還元できる。これらが(\ref{3.1})式にどのような変化をもたらすか考えれればよいのだが、(\ref{3.1})式には電荷密度、および電流密度に依存する式はなく、(\ref{3.1})式に代入する部分はないため、変更はない。

3−2　物質中におけるAmpere-Maxwellの法則の導出

それでは最後に，真空中のAmpere-Maxwellの法則

\begin{equation} \nabla \times \boldsymbol B(\boldsymbol r,t)=\epsilon_0\mu_0\frac{\partial \boldsymbol E(\boldsymbol r,t)}{\partial t}+\mu_0\boldsymbol j(\boldsymbol r,t)\label{3.5} \end{equation}

が，物質中でどのように変更されるのか考えてみよう。

ここで我々が考察しなければならないのは，磁化$\, \boldsymbol M\, $と電気分極$\, \boldsymbol P\, $が，(\ref{3.5})式にどのように影響を与えるのかということである。とはいえ，これら2つを同時に考察するのは少々面倒なので，ここからは2節に分けて考察する。

磁化の寄与

まず，磁化$\, \boldsymbol M\, $の寄与を考える。前ページ2で考察したように，磁化$\, \boldsymbol M(\boldsymbol r)\, $がつくる磁束密度は，その磁性体の内部を流れる体積電流密度$\, \boldsymbol j_M\, $と，表面を流れる表面電流密度$\, \boldsymbol i_M\, $ \begin{equation} \boldsymbol j_M=\nabla\times \boldsymbol M ,\quad \boldsymbol i_M=-\boldsymbol n\times \boldsymbol M\label{3.6} \end{equation} が作る磁束密度と同じである。そこで，この式を真空中のAmpere-Maxwellの法則(\ref{3.5})式の積分形に適用すると，

\begin{equation} \int_C \boldsymbol B_m\cdot d\boldsymbol \ell=\mu_0\int_{S'}\boldsymbol j_M\cdot \boldsymbol ndS+\mu_0 \int_{C'}\boldsymbol i_M\cdot \boldsymbol nd\ell' \label{3.7} \end{equation}

となる。ここで$\, C\, $は任意の閉ループ，$\, S\, $は$\, C\, $を境界とする任意の曲面，$\, C'\, $は磁性体の表面と$\, S\, $が交わる閉ループ$\, C'+C''\, $のうち，磁性体の表面部分に相当する部分，$\, S'\, $は$\, C'+C''\, $を境界とする$\, S\, $の一部である（下図）。また，$\, \boldsymbol n=\boldsymbol n(\boldsymbol r)\, $は曲面$\, S\, $における面ベクトルである。

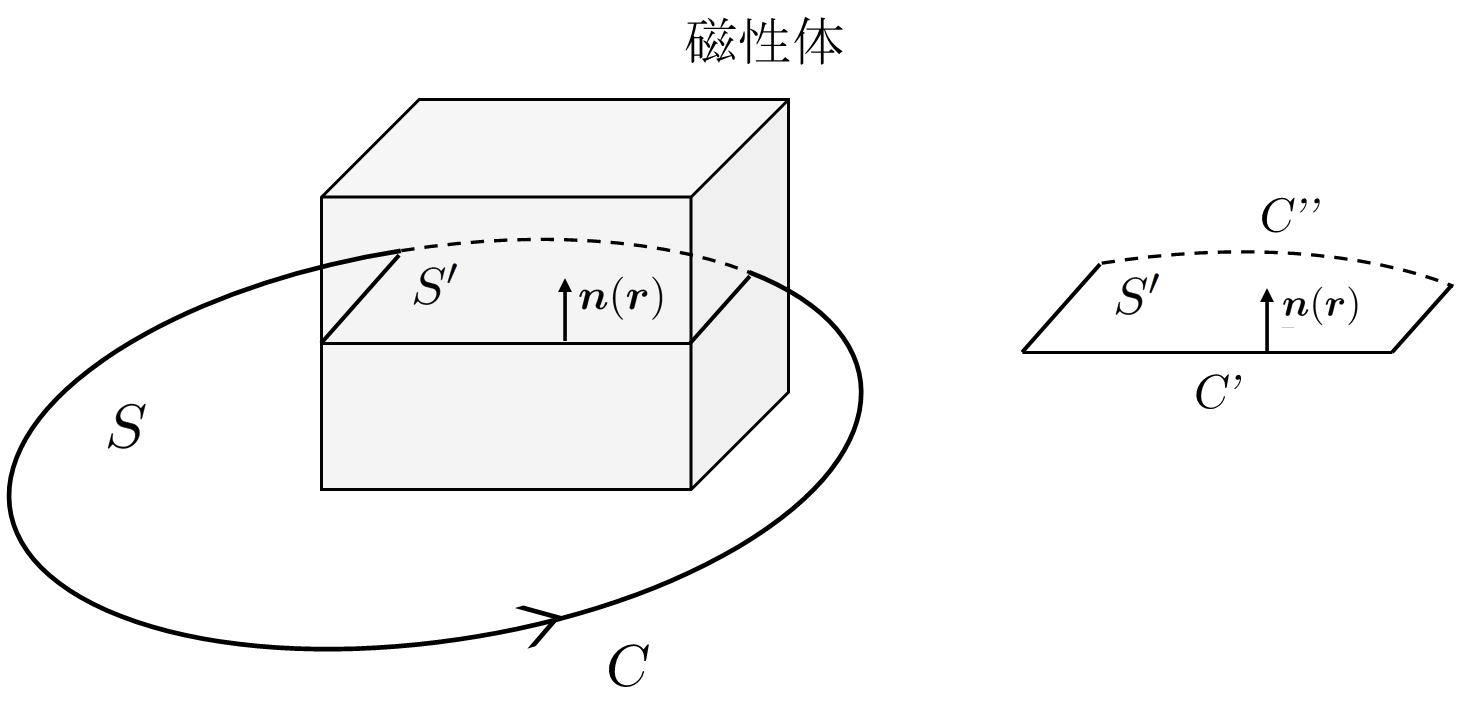
このとき，(\ref{3.7})式の右辺第1項の積分は，$\, S'\, $をつらぬく体積電流密度$\, \boldsymbol i_M\, $の面積分であり，第2項の積分は，表面電流密度$\, \boldsymbol j_M\, $のうち，$\, \boldsymbol n\, $に平行な成分を，$\, C'+C''\, $に沿って1周積分したものである。

(\ref{3.7})式に(\ref{3.6})式を代入すると，

\begin{equation} \int_C \boldsymbol B_m\cdot d\boldsymbol \ell=\mu_0\int_{S'}\boldsymbol (\nabla\times \boldsymbol M)\cdot \boldsymbol ndS+\mu_0 \int_{C'}\boldsymbol (-\boldsymbol n'\times \boldsymbol M)\cdot \boldsymbol nd\ell' \label{3.8} \end{equation}

となる。ここで$\boldsymbol n'$は磁性体の表面に対する面ベクトルである。

(\ref{3.8})の第1項は，ストークスの定理を用いて

\begin{equation} \mu_0\int_{S'}\boldsymbol (\nabla\times \boldsymbol M)\cdot \boldsymbol ndS =\mu_0\int_{C'+C''}\boldsymbol M \cdot d\boldsymbol \ell' \label{3.9} \end{equation}

とかける。第2項は，閉曲面$\, C'\, $を囲むベクトルを$\, \boldsymbol \ell'\, $とすれば，$\, \boldsymbol \ell'=-\boldsymbol n'\times \boldsymbol n\, $であることより，

\begin{equation} \begin{split} \mu_0 \int_{C'}\boldsymbol (-\boldsymbol n'\times \boldsymbol M)\cdot \boldsymbol nd\ell'&=\mu_0 \int_{C'}\boldsymbol M\cdot(\boldsymbol n'\times \boldsymbol n)d\ell'\\ &=-\mu_0 \int_{C'}\boldsymbol M\cdot d\boldsymbol \ell' \end{split} \label{3.10} \end{equation}

とかける。以上より，(\ref{3.8})式に(\ref{3.9})，(\ref{3.10})式を代入して，

\begin{equation*} \begin{split} \int_C \boldsymbol B_m\cdot d\boldsymbol \ell&=\mu_0\int_{C'+C''}\boldsymbol M \cdot d\boldsymbol \ell'-\mu_0 \int_{C'}\boldsymbol M\cdot d\boldsymbol \ell'\\ &=\mu_0\int_{C''}\boldsymbol M \cdot d\boldsymbol \ell'=\mu_0\int_{C}\boldsymbol M \cdot d\boldsymbol \ell\\ \end{split} \end{equation*}

となる。これを微分形に直すと \begin{equation} \nabla\times (\boldsymbol B_m-\boldsymbol M)=0\label{3.11} \end{equation} となるので，(\ref{3.11})と(\ref{3.5})式を足し合わせることにより，

\begin{equation} \nabla \times \big\{\big(\boldsymbol B_0+\boldsymbol B_m)-\boldsymbol M\big\}=\epsilon_0\mu_0\frac{\partial \boldsymbol E}{\partial t}+\mu_0\boldsymbol j\label{3.12} \end{equation}

となる。ここで$\, \boldsymbol B=\boldsymbol B_0+\boldsymbol B_m\, $は外部磁束密度$\, \boldsymbol B_0\, $と分極の結果生じた磁束密度$\, \boldsymbol B_m\, $を足し合わせた全磁束密度である。以上から，$\, \boldsymbol B=\mu_0\boldsymbol H + \boldsymbol M\, $を代入して磁場$\, \boldsymbol H\, $に書き換えることにより，(\ref{3.12})式は \begin{equation} \nabla \times \boldsymbol H(\boldsymbol r,t)=\epsilon_0\frac{\partial \boldsymbol E(\boldsymbol r,t)}{\partial t}+\boldsymbol j(\boldsymbol r,t)\label{3.13} \end{equation} とかける。これが磁性体の磁化$\, \boldsymbol M\, $の寄与を取り入れた，Ampere-Maxwellの法則である。

電気分極$\, \boldsymbol P\, $の寄与

最後に，電気分極$\, \boldsymbol P\, $の寄与について考える。

ここで，ある電気双極子モーメント$\, \boldsymbol p=q\boldsymbol d\, $が時間変化している状況を考えよう。このとき，電気双極子モーメントの位置を$\, \boldsymbol r'\, $とすれば，電荷$\, \pm q\, $の位置を$\, \boldsymbol r'\pm \boldsymbol d(t)/2\, $（複合同順）とおくことができる。するとこれは，$\, +q\, $の電荷が速度$\, \boldsymbol d'(t)/2\, $で移動し，$\, -q\, $の電荷が速度$\, -\boldsymbol d'(t)/2\, $で移動していることに相当するので，これは，全体として

\begin{equation*} \begin{split} \boldsymbol j_p(\boldsymbol r,t)&=+q\frac{\boldsymbol d'(t)}{2}\delta(\boldsymbol r-\boldsymbol r')-q\frac{-\boldsymbol d'(t)}{2}\delta(\boldsymbol r-\boldsymbol r')\\ &=q\boldsymbol d'(t)\delta(\boldsymbol r-\boldsymbol r')=\dot{\boldsymbol p}\delta(\boldsymbol r-\boldsymbol r') \end{split} \end{equation*}

の電流密度が流れていることに相当する。

ただ，やはりこれは電気双極子が1つあったときの話である。実際の誘電体ではたくさんの電気双極子があるので，それらを$\, \boldsymbol p_1,\boldsymbol p_2,\cdots,\boldsymbol p_n\, $（位置$\, \boldsymbol r_1,\boldsymbol r_2,\cdots , \boldsymbol r_n\, $）とする。そして，それらに対応する電流密度$\, j_P(\boldsymbol r,t)\, $を \begin{equation} \boldsymbol j_P(\boldsymbol r,t)=\sum_{全i}\dot{\boldsymbol p}\delta(\boldsymbol r-\boldsymbol r')\label{aa} \end{equation} とする。このとき，位置ベクトル$\, \boldsymbol r\, $に存在するある小さな空間$\, V_{\boldsymbol r}\, $内において(\ref{aa})を積分し，その値を体積$\, V\, $で割った値

\begin{equation} \frac{1}{V} \int_{V_{\boldsymbol r}} \boldsymbol j_P(\boldsymbol r',t)d^3\boldsymbol r'=\frac{1}{V} \int_{V_{\boldsymbol r}} \sum_i \dot{\boldsymbol p_i}\delta(\boldsymbol r'-\boldsymbol r_i)d^3\boldsymbol r'\label{bb} \end{equation}

を考える。(\ref{bb})式の左辺は，$\, V_{\boldsymbol r}\, $が微小ならば$\, \boldsymbol j_P(\boldsymbol r',t)\, $は一定と見なせるので

\begin{equation*} \frac{1}{V} \int_{V_{\boldsymbol r}} \boldsymbol j_P(\boldsymbol r',t)d^3\boldsymbol r'=\frac{1}{V} \int_{V_{\boldsymbol r}} \boldsymbol j_P(\boldsymbol r,t)d^3\boldsymbol r'=\boldsymbol j_P(\boldsymbol r,t) \end{equation*}

となり，値を変えない。一方で，(\ref{bb})式の右辺は，1ページで触れた式 \begin{equation*} \boldsymbol P(\boldsymbol r)=\frac{1}{V} \int_{V_{\boldsymbol r}} \sum_i \boldsymbol p_i\delta(\boldsymbol r-\boldsymbol r_i)d^3\boldsymbol r \end{equation*} により，電気分極$\, \boldsymbol P\, $を時間で偏微分したものとなる。以上より，(\ref{bb})式は \begin{equation} \boldsymbol j_P(\boldsymbol r,t)=\frac{\partial \boldsymbol P(\boldsymbol r,t)}{\partial t}\label{cc} \end{equation} とかける。以上より，これによってできる磁場$\, \boldsymbol H_p\, $は，(\ref{3.13})，(\ref{cc})式より， \begin{equation} \nabla\times \boldsymbol H_p=\frac{\partial \boldsymbol P(\boldsymbol r,t)}{\partial t}\label{dd} \end{equation} を満たす。以上より，(\ref{3.13})，(\ref{dd})式を足し合わせて，

\begin{equation} \nabla \times \big\{\boldsymbol H(\boldsymbol r,t)+\boldsymbol H_p(\boldsymbol r,t)\big\}=\epsilon_0\frac{\partial \boldsymbol E(\boldsymbol r,t)}{\partial t}+\frac{\partial \boldsymbol P(\boldsymbol r,t)}{\partial t}+\boldsymbol j(\boldsymbol r,t)\label{ee} \end{equation}

となるので，全磁場を$\, \boldsymbol H(\boldsymbol r,t)\, $，$\, \boldsymbol D(\boldsymbol r,t)=\epsilon_0\boldsymbol E(\boldsymbol r,t)+\boldsymbol P(\boldsymbol r,t)\, $とおいて式を書きなおして，以上より，

\begin{align} \nabla \times \boldsymbol H(\boldsymbol r,t)=\frac{\partial \boldsymbol D(\boldsymbol r,t)}{\partial t}+\boldsymbol j(\boldsymbol r,t)\label{uu} \end{align}

が成立する。これが，物質中におけるMaxwell-Ampereの法則である。

ちなみに、上の式からわかるように、電束密度の時間微分 \begin{align*} \frac{\partial \boldsymbol D(\boldsymbol r,t)}{\partial t} \end{align*} は、電流そのものではないものの、電流と同様の物理的意味を持つという（ちょっと不思議な）性質を持つ。このような意味で、電束密度の時間微分は変位電流と呼ばれる。